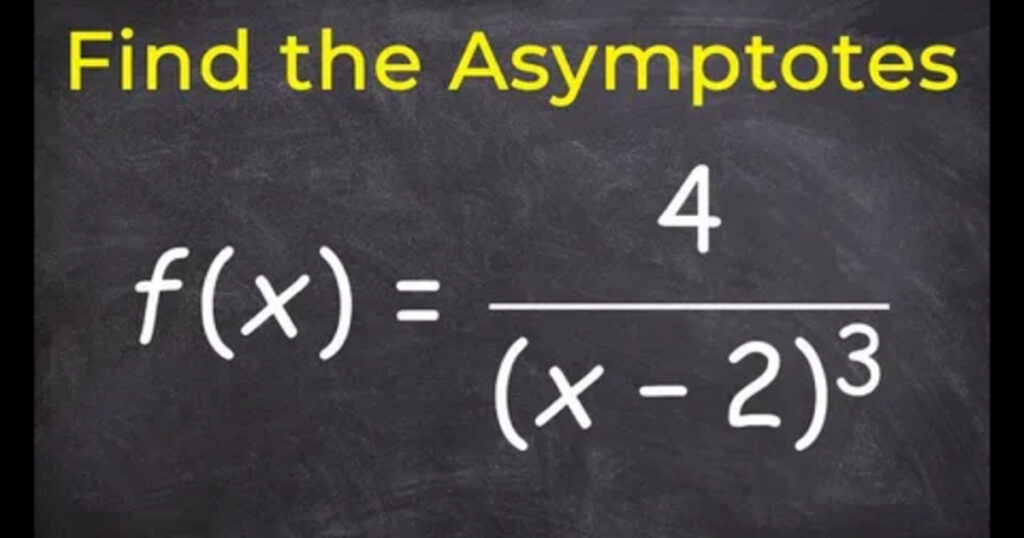How to Find Horizontal Asymptotes: Rational Function
What are Asymptotes in a Rational Function?
Definition of asymptotes: In mathematics, asymptotes are lines that a curve approaches but never quite reaches. In the context of functions, asymptotes represent values that the function gets close to as the input approaches a certain number.
Types of asymptotes in functions: There are mainly two types of asymptotes – vertical and horizontal. Vertical asymptotes occur where the function is undefined, while horizontal asymptotes show the value the function approaches as x approaches positive or negative infinity.
Importance of asymptotes in graphing: Asymptotes play a crucial role in graphing functions as they help in understanding the behavior of functions towards certain inputs. They provide valuable information about the trends and limits of the function.
Related Article: How many People can solve a Rubik’s Cube? Rubik Cube
How to Identify Vertical Asymptotes?
Understanding vertical asymptotes: Vertical asymptotes arise in functions when the denominator of a rational function becomes zero at certain points, leading to vertical lines that the graph approaches but does not cross.
Finding vertical asymptotes in a rational function: To find vertical asymptotes in a rational function, set the denominator equal to zero and solve for the values of x that make the denominator zero. These values will be the locations of the vertical asymptotes.
Steps to identify vertical asymptotes: Identify the values of x that make the denominator equal to zero. These values will be the vertical asymptotes of the function. Plotting these asymptotes on a graph helps in understanding the behavior of the function.
Methods to Find Horizontal Asymptotes
Definition of horizontal asymptotes: Horizontal asymptotes are horizontal lines that a function approaches as x tends to positive or negative infinity. They represent the long-term behavior of a function.
Techniques to find horizontal asymptotes: To find horizontal asymptotes, compare the degrees of the numerator and denominator of a rational function. If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0. If the degrees are equal, divide the leading coefficients to find the horizontal asymptote.
Examples of finding horizontal asymptotes: For a rational function where the degree of the numerator is less than the degree of the denominator, the horizontal asymptote will be the x-axis (y = 0). In cases where the degrees are equal, dividing the leading coefficients gives the value of the horizontal asymptote.
Related Article: How many People can solve a Rubik’s Cube? Rubik Cube
Comparing Horizontal and Vertical Asymptotes
Differences between horizontal and vertical asymptotes: Vertical asymptotes are vertical lines that represent the places where the function is undefined, while horizontal asymptotes are horizontal lines that the function approaches as x goes to infinity.
Relationship between horizontal and vertical asymptotes: Horizontal and vertical asymptotes provide insights into the behavior of the function at different points. While vertical asymptotes denote discontinuities, horizontal asymptotes show the long-term trends of the function.
How to analyze functions using both types of asymptotes: By considering both horizontal and vertical asymptotes, one can gain a comprehensive understanding of how a function behaves, both locally around specific points and globally as x approaches infinity.
Advanced Concepts in Horizontal Asymptotes
Exploring oblique asymptotes: In some cases, rational functions may have oblique asymptotes, also known as slant asymptotes. These occur when the degree of the numerator is exactly one more than the degree of the denominator.
Identifying end behavior in rational functions: The end behavior of a rational function is determined by its horizontal asymptotes. Understanding the long-term trends of the function near infinity helps in sketching accurate graphs.
Factors affecting the presence of horizontal asymptotes: The presence of horizontal asymptotes in rational functions depends on the degrees of the numerator and denominator. The relationships between these degrees dictate whether horizontal asymptotes exist and their values.
How to Find Horizontal Asymptotes: Rational Function
What is a Horizontal Asymptote in a Rational Function?
Definition of horizontal asymptote
A horizontal asymptote in a rational function is a horizontal line that the graph of the function approaches as x tends towards positive or negative infinity. This line indicates the behavior of the function at the extremes of its domain.
Characteristics of horizontal asymptotes
Horizontal asymptotes can be identified by analyzing the degrees of the numerator and denominator of the rational function. They play a crucial role in understanding the long-term behavior of the function.
Importance of horizontal asymptotes in graphing
Understanding horizontal asymptotes is essential in graphing rational functions accurately. They help in visualizing how the function behaves as x approaches infinity or negative infinity.
How to Identify Horizontal Asymptotes of Rational Functions
Finding horizontal asymptotes algebraically
To find horizontal asymptotes algebraically, compare the degrees of the numerator and denominator of the rational function. If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0.
Using limits to determine horizontal asymptotes
Calculating the limit of the function as x approaches infinity or negative infinity helps in identifying horizontal asymptotes. If the limit exists and is a real number, it represents the horizontal asymptote.
Graphical representation of horizontal asymptotes
Graphing the rational function visually can also help in determining the horizontal asymptotes. They appear as the horizontal lines that the function approaches but never crosses.
Key Differences Between Horizontal and Vertical Asymptotes
Definition of vertical asymptote
Unlike horizontal asymptotes, vertical asymptotes occur where the denominator of a rational function is equal to zero, causing a vertical line that the function approaches but never crosses.
Comparison of end behaviors related to horizontal and vertical asymptotes
Horizontal asymptotes indicate the function’s behavior at infinity, whereas vertical asymptotes show discontinuities in the function. They have distinct effects on the graph’s end behavior.
Distinguishing features in the graph of the function
The graph of a function may have multiple vertical asymptotes but typically only one horizontal asymptote. Vertical asymptotes are associated with abrupt changes in the function’s value.
Strategies to Find Horizontal Asymptotes in College Algebra
Techniques to identify horizontal asymptotes in rational functions
In college algebra, students learn various methods to identify horizontal asymptotes, such as degree analysis and limit calculations.
Applying degree analysis to determine horizontal asymptotes
Analyzing the degrees of the numerator and denominator helps in determining the behavior of a rational function towards infinity, aiding in finding horizontal asymptotes.
Practical examples of finding horizontal asymptotes
Solving real-world problems and practicing with different rational functions helps students in mastering the skill of finding horizontal asymptotes accurately.
Challenges in Identifying Horizontal Asymptotes
Dealing with complex rational functions
Complex rational functions with multiple terms or higher-degree polynomials can pose challenges in identifying horizontal asymptotes due to the complexity of the function.
Factors affecting the identification of horizontal asymptotes
Factors such as the presence of slant asymptotes or ambiguous cases can complicate the process of identifying horizontal asymptotes in certain rational functions.
Strategies to overcome common mistakes in finding horizontal asymptotes
Overcoming common errors in finding horizontal asymptotes involves thorough practice, understanding the underlying concepts, and seeking help when encountering difficulties.
Q: What is a horizontal asymptote of a rational function?
A: A horizontal asymptote of a rational function is a horizontal line that the function approaches as the input values become very large or very small.
Q: How can I find the horizontal asymptote of a rational function?
A: To find the horizontal asymptote of a rational function, compare the degrees of the numerator and the denominator and determine how they affect the function’s behavior as x approaches positive or negative infinity.
Q: When does a rational function have a horizontal asymptote?
A: A rational function has a horizontal asymptote when the degree of the numerator is less than or equal to the degree of the denominator.
Q: How do vertical and horizontal asymptotes differ in a rational function?
A: Vertical asymptotes are values of x where the function is undefined, while horizontal asymptotes are lines that the function approaches as x goes to infinity or negative infinity.
Q: What is the relationship between the leading terms of a rational function and its horizontal asymptote?
A: The horizontal asymptote of a rational function is determined by the ratio of the leading coefficients of the highest degree terms in the numerator and denominator.
Q: Can a rational function cross its horizontal asymptote?
A: A rational function will never cross its horizontal asymptote; it will approach the asymptote as x approaches infinity or negative infinity.
Q: How can I identify horizontal asymptotes in the graph of a rational function?
A: To identify horizontal asymptotes in the graph of a rational function, analyze the end behavior of the function as x approaches positive or negative infinity.