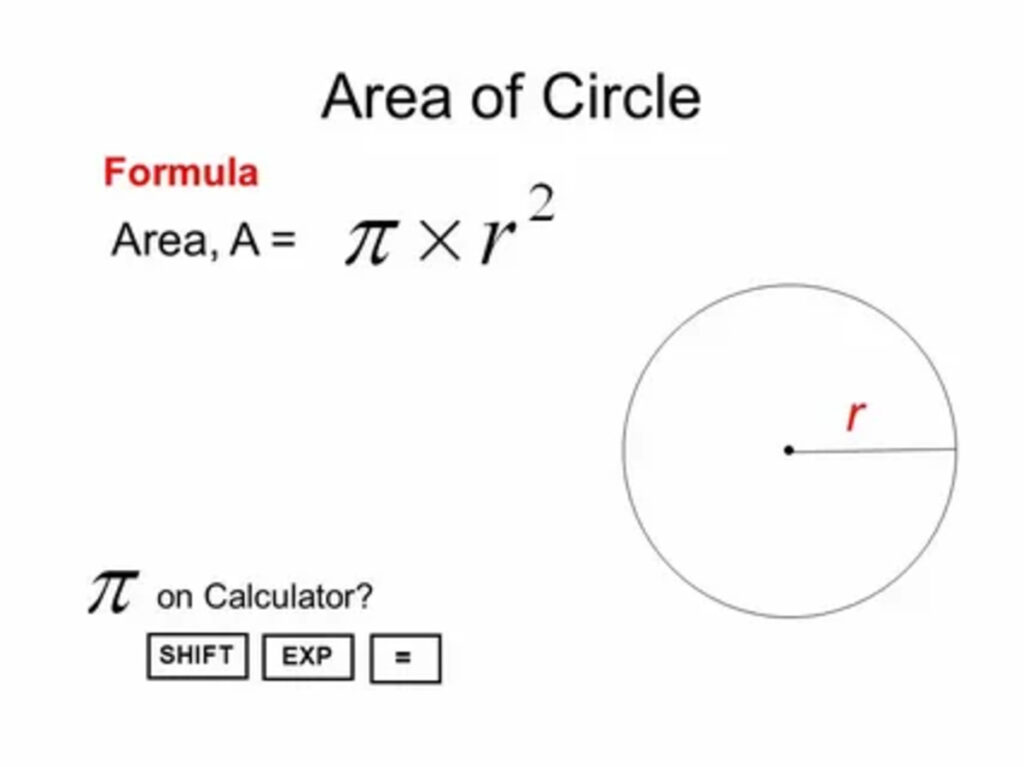
How to Find the Area of a Circle Calculator Formula

Calculating the area of a circle is a fundamental concept in math and geometry that requires understanding the relationship between the radius and diameter of a circle. The formula for calculating the area of a circle involves the use of the mathematical constant Pi, denoted by the symbol π.

What is the Formula for Calculating the Area of a Circle?

To determine the area of a circle, you need to know the radius of the circle. The formula for finding the area of a circle is A = πr^2, where A represents the area, π is approximately equal to 3.14159, and r is the radius of the circle.

Understanding the Concept of Pi

Pi is an irrational number that represents the ratio of the circumference of a circle to its diameter. It is a crucial constant in mathematics and is used in various formulas involving circles, spheres, and trigonometric functions.

Related Article: How to Find Horizontal Asymptotes: Rational Function

Using the Radius in the Area Formula

The radius of a circle is the distance from the center of the circle to any point on its boundary. When calculating the area of a circle, the radius is squared and multiplied by Pi to obtain the total area enclosed by the circle.

Calculating the Area with the Formula

To find the area of a circle using the formula, simply square the radius and multiply it by Pi. The resulting value will give you the area of the circle in square units, such as square inches, square centimeters, or square meters.

How to Find the Circumference of a Circle?

In addition to the area, the circumference of a circle is another crucial measurement that helps determine the distance around the circle. The circumference is directly related to the diameter of the circle and can be calculated using the formula C = πd, where C represents the circumference and d is the diameter of the circle.

Definitions of Circumference and Diameter

The circumference of a circle is the total length of its boundary, while the diameter is the distance across the circle passing through its center. The relationship between the circumference and diameter is essential in circle calculations.

Using the Circumference Formula

To find the circumference of a circle, multiply the diameter by Pi. This simple formula allows you to determine the distance around the circle, which is useful in various mathematical and real-world applications.

Practical Example of Finding the Circumference

For example, if a circle has a diameter of 10 units, you can find its circumference by multiplying 10 by Pi, giving you a total circumference of approximately 31.4159 units. This calculation helps in understanding the size and proportions of circles in different contexts.

Related Article: How to find Perimeter of a Rectangle?

What is the Relationship Between the Radius and Diameter in a Circle?

The radius and diameter of a circle are interconnected measurements that provide valuable insights into the circle’s dimensions. The diameter of a circle is always twice the length of its radius, making them crucial in circle calculations.

Understanding the Relationship Between Radius and Diameter

The radius is half the length of the diameter in a circle. This relationship is important when converting between radius and diameter or when calculating circle properties like area and circumference.

Calculating Radius from Diameter

To find the radius of a circle from its diameter, simply divide the diameter by 2. This straightforward calculation helps in determining the radius when the diameter is known.

Comparing Radius and Diameter in Circle Measurements

When comparing the radius and diameter of a circle, it’s essential to remember that the diameter is the longest chord that can be drawn inside the circle, passing through the center, while the radius is from the center of the circle to its boundary.

How to Calculate the Surface Area of a Circle?

While the area of a circle refers to the space enclosed by its boundary, the surface area encompasses the area inside the circle and the circular boundary itself. Calculating the surface area of a circle involves specific formulas derived from its properties.

Defining Surface Area in the Context of a Circle

The surface area of a circle is the total area of the circle’s boundary and the space enclosed within it. It is a critical measurement in geometry and is used in various applications related to curved surfaces.

Deriving the Formula for Surface Area of a Circle

The formula for the surface area of a circle involves the radius of the circle and specific geometric principles. By utilizing the properties of circles and geometrical calculations, you can determine the surface area accurately.

Practical Application of Calculating Surface Area

Understanding the surface area of a circle is essential in fields such as engineering, architecture, and physics. By knowing how to calculate the surface area, you can design structures, analyze shapes, and solve practical problems involving circular surfaces.

Why is Knowing the Area and Circumference of a Circle Important?

The area and circumference of a circle play significant roles in various disciplines and everyday scenarios. Understanding these measurements and their formulas is crucial for making informed decisions and solving problems efficiently.

Applications of Area and Circumference in Real-life Situations

The area and circumference of a circle are used in real-world applications such as calculating land area, designing circular objects, and determining distances around circular paths. These measurements have practical implications in many industries and activities.

Importance of Circle Measurements in Geometry and Engineering

In geometry and engineering, circle measurements are fundamental to understanding shapes, angles, and dimensions. Circles are prevalent in structural designs, mechanical systems, and architectural blueprints, making knowledge of their properties essential.

How Area and Circumference Calculations are Used in Various Fields

From calculating the area of a circular garden to determining the circumference of a roundabout, circle measurements are ubiquitous in our daily lives. Professionals in fields such as mathematics, physics, and urban planning rely on accurate circle calculations for their work.